Das Dreieck, vor allem das gleichseitige ist neben dem Kreis, der auch ein aufgeblasener Punkt sein könnte, eine elementare Form der Fläche. Die Fläche kann durch zwei Geraden, eindimensionalen Linien, die sich schneiden, definiert werden. Von diesem Schnittpunkt gehen zwei Halbgeraden aus oder zwei Strecken (mit Anfang im Schnittpunkt und einem Endpunkt) die als Vektoren aufgefasst werden können, die dann die Ebene aufspannen (so wird die Fläche korrekt bezeichnet, da eine Fläche auch gekrümmt sein kann und die gedachte Fläche hier eben eben ist). Verbinden sich diese eindimensionalen Linien mit einer dritten und bilden eine geschlossene Form, entsteht das Dreieck. Und neben dem Quadrat (aus zwei gleichschenkligen Dreiecken) und dem Sechseck (aus sechs gleichseitigen Dreiecken) ist es eine flächendeckend Form (genauer es gibt nur drei mögliche regelmäßige Parkettierungen mit identischen regelmäßigen Polygonen). Der einzige Schönheitsfehler, um diese ‚Aufgabe‘ zu erfüllen, benötigt man zwei verschieden gedrehte Formen, die miteinander eine Raute bilden (dies verschobene Quadrat gilt nicht als regelmäßiges Polygon).

Für diese Graphik hat mit Perplexity ein kleines Python-Programm geschrieben.

Das ist deshalb interessant, weil Jacob L. S. Bellmund und seine Kollegen festgestellt haben, das unsere räumlich Wahrnehmung über solche Muster erfolgt. ‚Hexadirektionale Kodierung des visuellen Raums im menschlichen entorhinalen Kortex‘ nennt man das (in der Veröffentlichung: ‚Hexadirectional coding of visual space in human entorhinal cortex‚ und genaugenommen besteht unsere kognitive Raumrepräsentanz aus Sechsecken, die in dWürfeler Mitte von sechs Dreiecken liegen) und darüber hinaus spannen wir auch ‚Kategorien‘ in solche virtuellen Ebenen, erstaunlicherweise stellen wir solche Muster dann aber häufige als orthogonale System dar (vergl. dazu Bellmunds Beitrag in Natur, der leider hinter einer Bezahlschranke liegt). Der rechte Winkel, der in der Natur so selten vorkommt, hat sich in das virtuelle Raster des Menschen eingebrannt, es ist auch ein Erkennungszeichen für Menschengemachtes (also sogenannte Artefakte) und es lässt sich problemlos in den dreidimensionalen Raum erweitern (vergl. Würfel).

Mit diesem python-generierten Bild verlassen wir aber das Dreieck.

Es bleibt noch anzumerken, das der einfachste platonischer Körper, der Tetraeder ebenfalls aus gleichseitigen Dreiecken besteht. Mit dem Tetraeder kann der dreidimensionale Raum aufgespannt werden.

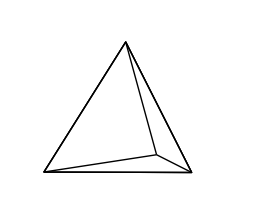
Für dieses Bild musste ich den Perplexity Code von Le Chat verbessern lassen, in der Python-Anwendung kann ich den Körper mit der Maus rotieren, es war gar nicht so leicht die Winkel so zu treffen. Die verkürzte Darstellung der y-Achse im 45° Winkel nennt man Axonometrie und wer es kennt: hier tritt auch der Effekt auf, der vom Necker-Würfel bekannt ist, die mittlere Ecke erscheint entweder hinter der vorderen Ebene zu sein oder nach vorne zu springen (beim Würfel ist der Effekt aber besser zu erkennen).